Experimento Interactivo 5 de Dispositivos Cuánticos

Efecto Stark confinado

El efecto Stark confinado ocurre cuando se aplica un campo eléctrico uniforme normal a las intercaras de un pozo cuántico muy profundo. La presencia del campo eléctrico modifica tanto las funciones envolventes como la energía de los niveles. En particular, afecta al borde de absorción de luz al cambiar la energía de las transiciones permitidas entre estados de la banda de conducción y de la banda de valencia. Lógicamente este efecto es de aplicación inmediata en dispositivos optoelectrónicos.

El sistema que vamos a considerar es un pozo cuántico de GaAs-AlAs, donde vamos a estudiar el efecto de un campo eléctrico sobre el estado fundamental de la banda de conducción, aplicado a lo largo de la dirección de crecimiento. El nivel de energía es tanto más bajo cuanto más ancha sea la lámina de GaAs, por lo que la hipótesis de confinamiento de los estados es razoble. En caso contrario, los electrones pueden escapar del pozo por efecto túnel cuando se aplica el campo, algo que no vamos a considerar en este Ejercicio.

La ecuación de Ben Daniel-Duke para la función envolvente es entonces

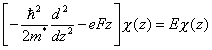(1)

cuando el momento transversal es nulo y z indica la dirección de crecimiento (perpendicular a las láminas de los semiconductores). F indica el valor del campo eléctrico. La función envolvente debe anularse en z=±a/2 si consideramos barreras infinitas.

Resulta conveniente hacer el cambio de variable u=z/a e introducir las cantidades V₀=eFa y

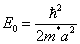
que tiene dimensiones de energía. De hecho, en ausencia de campo aplicado los niveles de energía vienen dados por

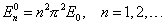
donde el superíndice indica la ausencia de campo aplicado. Con estos cambios, la ecuación para la función envolvente satisface la ecuación

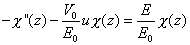(2)

que admite solución exacta en térmnos de las funciones de Airy. No obstante, en el presente estudio vamos a presentar la resolución del problema mediante técnicas perturbativas así como numéricas, que son útiles porque permiten abordar otras situaciones más complejas.
 

Cálculo perturbativo

Para analizar el problema desde el punto de vista de la teoría de perturbaciones tenemos que admitir que el campo es débil (posteriormente analizaremos con más detalle esta condición) y conocer los estados del pozo cuántico en ausencia de campo. El estado fundamental no perturbado es simplemente

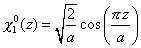(3)

La corrección de primer orden a su energía cuando se aplica el campo es

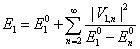(4)

siendo

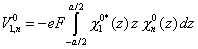(5)

que se anula salvo que la función envolvente tenga paridad impar. Por tanto, tenemos que evaluar los siguientes elementos de matriz

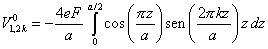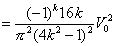
	(6)

La serie resultante se puede sumar exactamente y el resultado conduce a una expresión que se puede aproximar muy bien por

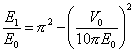(7)

El rango de validez de este cálculo se averigua comparando dos magnitudes esenciales: diferencia de niveles no perturbados y corrección del primer nivel debido a la perturbación. Lógicamente la primera magnitud debe ser mucho mayor que la segunda. Puesto que ambas magnitudes son ya conocidas, una sencillo estimación nos lleva a la conclusión de que el campo aplicado puede llegar a ser muy alto y la aproximación perturbativa sigue siendo válida. Sin embargo, los pozos cuánticos reales distan mucho de esta situación, básicamente porque el electrón escapa del pozo por efecto túnel dado que las barreras reales tienen una energía finita.
 

Cálculo numérico

Para realizar el cálculo numérico dividimos el intervalo [-1/2,1/2] en N+1 segmentos de longitud s=1/(N+1). La discretización de la derivada segunda en los puntos u=ns-1/2 conduce a la siguiente ecuación en diferencias para la función envolvente evaluada en dichos puntos

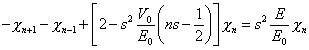(8)

con las condiciones de contorno

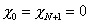(9)

En definitiva, necesitamos diagonalizar una matriz tridiagonal, y para ello existen numerosas rutinas muy eficientes, que son las que emplearemos para obtener el estado fundamental.
 

Fuerza de oscilador

Cuando hacemos que un láser incida en dirección paralela a las intercaras, se pueden producir transiciones entre los dos primeros estados del pozo cuántico (no son las únicas, claro está). La intensidad de la correspondiente línea de absorción viene determinada por la fuerza de oscilador

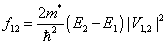(10)

siendo

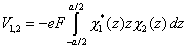(11)

En ausencia de campo uniforme aplicado se puede calcular su valor sin grandes difucultades, que resulta ser 0.96. Cuando se aplica campo se espera que dicho valor se reduzca porque entonces hay más transiciones permitidas ya que se rompe la simetría existente en ausencia de campo. El cálculo numérico expuesto permite también obtener sin dificultad el valor de la fuerza de oscilador entre los dos primeros estados del pozo cuántico.

Desarrollo del ejercicio

El sistema elegido para hacer el estudio del efecto Stark confinado es un pozo cuántico de GaAs-AlAs de anchura a, donde suponemos que la altura de la barrera es infinita. La masa efectiva de los electrones es m^*=0.067m,siendo m la masa del electrón libre.

Pulsando sobre el botón se accede a un programa  que permite determinar la energía y la función envolvente de los estados confinados. En la gráfica de la derecha se representa la energía del estado fundamental (línea azul) en función del campo eléctrico aplicado y se compara el cálculo perturbartivo (línea roja). Además obtiene el valor de la fuerza de oscilador f₁₂.