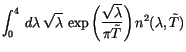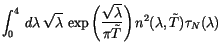Experimento Interactivo 4 de Física del Estado Sólido

Conductividad térmica de una cadena desordenada

En una cadena desordenada de átomos, los modos normales de vibración son localizados, esto es, sólo los átomos de una pequeña porción del sistema están vibrando, mientras que el resto de los átomos permanece en reposo. Este hecho es muy relevante si queremos estudiar sus propiedades de conducción térmica, pues la existencia de modos localizados hace que la energía que se aporte a uno de los extremos no podrá ser transportada por dichos modos.

Comenzaremos el análisis reescribiendo la ecuación para los desplazamientos atómicos en forma matricial de la siguiente manera

(1)

Sin más que iterar la ecuación anterior encontramos que

(2)

donde T(N) es la matriz de transferencia de toda la cadena, y las cantidades U₀ y U_N+1 vienen especificadas por las condiciones de contorno. Un sencillo cálculo permite obtener el coeficiente de transmisión en términos de los elementos de esta matriz

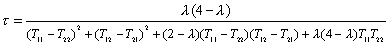
siendo T_ij=T_ij(N) los elementos de la matriz de transferencia. Estos elementos se pueden calcular recurrentemente mediante la relación

			(3)

Conocido el coeficiente de transmisión para cada valor de se puede calcular la conductividad térmica de la cadena a una determinada temperatura T como

(4)

donde se ha introducido la notación

(5)

siendo la función distribución de Bose y K_B la constante de Boltzmann. Aquí es la frecuencia máxima de la vibraciones armónicas, cuya relación con la temperatura de Debye es .

Llamando a la temperatura en unidades de la temperatura de Debye, teniendo en cuenta que , se encuentra que la conductividad térmica de una cadena desordenada puede reescribir, salvo constantes, como

(6)

			(7)

Desarrollo del ejercicio

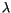Pulsando sobre el botón se accede a un programa que calcula y representa gráficamente el coeficiente de transmisión en función de . En una segunda gráfica se representa la conductividad térmica en función de la temperatura, expresada ésta en términos de la temperatura de Debye. El cálculo de esta segunda curva puede llevar algo de tiempo, por lo que se recomienda paciencia.