Material Adicional

Precisión finita

Cuando se iteran las transformaciones del panadero y de Arnold muchas veces, se observa que los puntos comienzan a mostrar cierta regularidad y, finalmente, se concentran en el origen. Ello es debido a la precisión finita con la que se realizan los cálculos y, más concretamente, al uso de la operación (módulo 1).

Este efecto es fácil de ilustrar en la transformación del panadero, y para ello necesitamos escribir los números en sistema binario. Por ejemplo, 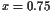se escribe en binario como:

En la transofrmación del panadero en la coordenada 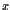se multiplica por 2 y posteriormente se toma el (módulo 1) de la misma. La aplicación de la multiplicación por 2 en la representación binaria no es más que despazar el punto decimal un lugar hacia la derecha:

Posteriormente, la aplicación de la operación (módulo 1) elimina los dígitos a la izquierda del punto decimal:

Como vemos, una aplicación de la transformación del panadero nos ha eliminado un dígito. Como los números reales se representan en los ordenadores mediante un número finito de dígitos, la aplicación sucesiva de la transformación nos deja sin dígitos significativos. Cualquier número representado por 8 bytes (como el tipo long de JAVA) tiene en binario como máximo 64 ceros y unos. Así pues, la aplicación de la transformación del panadero 64 veces deja al número sin dígitos significativos.

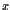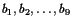Por ejemplo, consideremos un valor de cuya precisión en binario es de 9 dígitos. Llamemos a estos 9 dígitos . Por tanto, 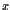en representación binaria es:

Entonces, tras aplicaciones de la transformación del panadero tendremos:

Como se oberva, cualquier coordenada 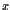acaba en 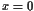tras múltiples aplicaciones de la transformación del panadero.

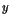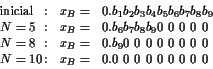
Algo similar sucede en la dirección : la división por 2 en binario simplemente mueve el punto decimal un lugar hacia la izquierda y los dígitos significativos se pierden por la izquierda.