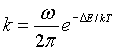Experimento Interactivo 8 de Sistemas fuera del Equilibrio

Procesos de activación: Ley de Arrhenius

Hemos visto en el experimento 7 el comportamiento de partícula brownianas en potenciales externos. Este comportamiento es la base de la llamada teoría de ritmos de activación que estudia los procesos de activación, es decir, cómo un sistema físico puede escapar de un estado metaestable gracias a las fluctuaciones térmicas.

Hay muchos fenómenos en física, química y biología que relacionados con este problema. Pensemos que en la mayoría de las reacciones químicas los productos iniciales están en estados metaestables, es decir, en mínimos locales de la energía libre, de los cuales escapan debido a fluctuaciones térmicas. El grado de avance de estas reacciones químicas se pueden representar a menudo por un grado de libertad químico que es equivalente a una partícula browniana en una dimensión y sometida a un potencial de dos pozos.

Veremos después que el ritmo de estos procesos de activación es proporcional al factor de Arrhenius :  , que explica el comportamiento en función de la temperatura de muchas reacción químicas y procesos biológicos, tan variados como el canto de los grillos o la intermitencia en la luz de las luciérnagas.

En el applet siguiente se pueden observar partículas de este tipo. Se puede variar el número de ellas, la temperatura y, a través del parámetro amplitud, la diferencia de energía entre los dos pozos. En la gráfica de la derecha se muestra cómo el número de partículas en el pozo metaestable disminuye en función del tiempo. La teoría de los ritmos de activación trata de encontrar la forma de esta curva.

En su versión más simple, la teoría supone que el número de partículas que abandonan el pozo es proporcional al número de partículas que hay en él. Por tanto, si  es el número de partículas que hay en l pozo metaestable en el instante t, tendremos;

                                      (1)

en donde k es el llamado ritmo de transición o ritmo de activación, y es la probabilidad de que una partícula abandone el pozo, es decir, la probabilidad de que cruce el máximo del potencial hacia la izquierda.

Para estimar el ritmo de activación podemos suponer que las partículas que se encuentran en el pozo metaestable están en equilibrio. Por tanto, la probabilidad de que una partículas se encuentre en el punto que separa los dos pozos, , es:

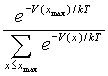
Recordemos  que en nuestra simulación las partículas se encuentran en una red de parámetro espaciada y saltan en intervalos de tiempo  de acuerdo con la dinámica de Metrópoli (ver experimento 7). El sumatorio se extiende por ello a todos los sitios de la red que están a la izquierda del punto que separa los dos pozos. De las partículas que se encuentran en  sólo la mitad se dirigen hacia la derecha y salen por tanto del pozo metaestable. Por tanto, el ritmo de activación para nuestro ejemplo será:

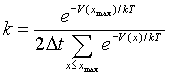                           (2)

en donde hemos tenido en cuenta la discretización temporal de nuestra simulación. El comportamiento del número de partículas en  el pozo metaestable será:

                (3)

Con k dado por la ecuación (2). En el applet se compara la curva teórica (3) con el resultado de la simulación.

En problemas en donde el tiempo y el espacio son continuos, la expresión (2) es:

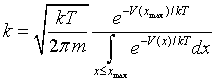           (4)

es decir, el sumatorio se sustituye por una integral y el factor , que provenía del número de partículas que, estando en  saltan hacia la izquierda por unidad de tiempo, se sustituye por el valor medio de la velocidad de las partículas que salen:

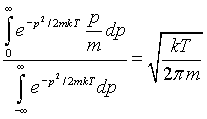
Para temperaturas bajas  ( ), el denominador de (4) se puede aproximar por:

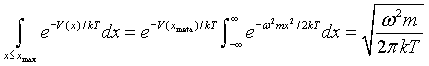      (5)

en donde hemos sustituido el potencial por su aproximación armónica en el mínimo del pozo metaestable:

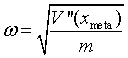                      (6)

Introduciendo (5) en (4) se llega a la bien conocida expresión de Arrhenius para los ritmos de activación: