Experimento Interactivo 5 de Sistemas fuera del Equilibrio

Reacciones quimicas; modelo de Maginu

Cuando una reacción química espacialmente extendida entre varias especies está fuera del equilibrio puede mostrar un comportamiento muy variado, dependiendo del tipo de reacción química y de la velocidad de difusión de las especies en relación con la velocidad de reacción. Por ejemplo, si el sistema se mantiene homogéneo (porque la reacción química se produce a un ritmo más lento que la difusión), el sistema puede tener uno o varios estados estacionarios, y en la evolución temporal puede seleccionar uno de ellos, oscilar periódicamente entre ambos o incluso mostrar comportamiento caótico. Por el contrario, si el sistema no se mantiene homogéneo (porque la difusión es lenta), el comportamiento puede ser todavía mucho más rico: se pueden producir anillos, ondas espirales, turbulencia o patrones de Turing.

Desde un punto de vista microscópico, las colisiones moleculares y las reacciones dan lugar a fluctuaciones que son importantes en la descripción del sistema. Esta práctica pretende estudiar las mismas.

Las especies que reaccionan evolucionan siguiendo un conjunto de ecuaciones de la forma:

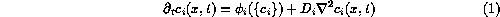
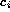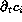donde indica la concentración de la especie i--ésima en el punto x en el instante t. Cada ecuación consta un término de evolución temporal, , otro que describe la difusión 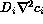, y, finalmente, la reacción química que se describe por 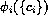que será, en general, una función no lineal de las concentraciones de las especies .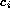

Cuando el sistema se mantiene homogéneo, se pueden eliminar los términos de difusión, 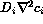, y las soluciones para las concentraciones de equilibrio son las soluciones estables del conjunto de ecuaciones:

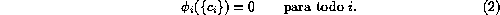
En esta práctica hemos implementado el llamando modelo de Maginu, que es un conjunto de ecuaciones de reacción-difusión para dos especies, descrito por:

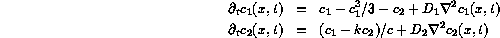
en el que las constantes k y c son arbitrarias con las restricciones: c>0 y 0<k<1. Para simplificar el modelo, tomamos 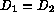, y elegimos como único paramétro independiente la constante s, que esencialmente mide la relación entre el término de difusión y el de reacción química. Para valores pequeños de s los términos de reacción son más importantes que la difusión (la reacción es rápida), mientras que para s grande, la reacción es lenta, así que el sistema se mantiene homogéneo gracias al término de difusión. 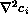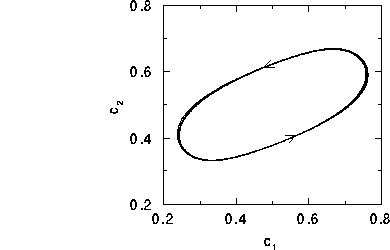Por tanto, las concentraciones de las especies no dependen de la posición y el término puede eliminarse, y las ecuaciones resultantes, 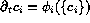describen un ciclo límite, mostrado en la figura.

El applet simula, mediante un autómata celular, un modelo microscópico de la reacción anteriormente descrita. Se puede elegir el parámetro de escala, s, y la especie que se quiere visualizar, o bien la diferencia entre las dos. Si el parámetro s es grande, la reacción evoluciona lentamente, y el término de difusión homogeneiza el sistema. Por ello, se observa una alternancia entre cada una de las especies y el sistema describe un ciclo amplio en el espacio , como el mostrado en la figura 1. Por el contrario, si s es pequeño, la difusión no es capaz de atenuar las fluctuaciones locales, así que sólo se observan pequeñas regiones coherentes, y el ciclo en el espacio 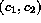es muy pequeño.

Aunque en este applet no se muestra, si 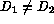, aparecen estructuras de Turing de tipo filamentoso para ciertos valores de los coeficientes de difusión.