Experimento Interactivo 7 de Sistemas fuera del Equilibrio

Difusión en un potencial externo

Hemos visto en el experimento 6 el comportamiento de la partícula browniana y su origen microscópico. En éste y en los experimentos siguientes, vamos a estudiar algunos fenómenos interesantes que ocurren cuando una partícula browniana se encuentra inmersa en un campo de fuerzas , que deriva de un potencial   .

Un caminante aleatorio, es decir, una partícula que se mueve en una red unidimensional y salta con probabilidad 1/2 a la izquierda o la derecha, es un modelo apropiado para el movimiento browniano en una dimensión y en ausencia de potencial externo. Cuando la partícula se encuentra en un potencial externo, hay que modificar las probabilidades de salto de un sitio  a sus vecinos  de la siguiente forma:

Ésta es la llamada dinámica de Metrópoli, en la que la probabilidad de que se dé un salto es 1/2 sólo si la energía decrece en el salto. Si la energía crece, entonces la probabilidad del salto es proporcional al factor de Boltzmann, que depende de la relación entre la energía ganada y la energía térmica kT.  Es decir, la partícula puede ganar una energía potencial del orden de kT debido a fluctuaciones térmicas. cuando la temperatura es cercana al cero absoluto, la dinámica hace que las partículas se muevan siempre hacia donde decrece la energía y acaben en un mínimo del potencial. Por el contrario, si la temperatura es muy alta las partículas apenas sienten el potencial y se mueven con probabilidad 1/2 hacia la derecha y la izquierda.

Si una partícula se mueve de acuerdo con las probabilidades de salto descritas en la ecuación (1), entonces su distribución de probabilidad estacionaria es el estado de Boltzmann:

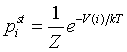                               (2)

por lo que el modelo reproduce correctamente la relajación al equilibrio térmico. Si, en lugar de una única partícula, tenemos un gran número N de partículas brownianas independientes, entonces el número de partículas en un sitio i será, en el estado estacionario, vendrá dado, salvo fluctuaciones, por . Pro tanto, la expresión (2) se puede entender como distribución de probabilidad para una partícula o, salvo el factor N, como densidad de partículas.

En el applet siguiente se puede experimentar con el movimiento de un gran número de partículas brownianas independientes que se mueven en un potencial cuya forma puede elegirse entre una parábola, un diente de sierra simétrico y uno asimétrico. Se puede variar también la temperatura y ver los resultados de dicha variación en tiempo real. En la figura izquierda se muestran las partículas moviéndose en el potencial elegido y en la derecha un histograma realizado sobre unas 200 unidades de tiempo. En la mayoría de los equipos, este tiempo es suficientemente pequeño como para considerar el histograma instantáneo. Se ha realizado sobre 200 unidades de tiempo en lugar de sobre una sola para aumentar la estadística. En la figura de la derecha se muestra también la energía térmica kT  en la misma escala que el potencial, de modo que pueda compararse con la energía potencial en cada punto del intervalo.

En la gráfica de la derecha se dibuja el histograma, convenientemente normalizado, y el estado de Boltzmann (2). La escala de esta gráfica se ha determinado de modo que el máximo del eje vertical coincida con el máximo del estado de Boltzmann.

El  applet ilustra la relajación al equilibrio de este gas ideal de partículas brownianas. Así mismo, muestra cómo las fluctuaciones térmicas son del orden kT y que, en el equilibrio, pocas partículas pueden adquirir energías superiores a este valor.