Modelo de Ben Daniel-Duke

Para estudiar los estados electrónicos en las heterouniones supondremos que son planas, abruptas y que las funciones de Bloch en ambos semiconductores, A y B, cerca de los bordes de las bandas son iguales. Esta última consideración es muy aceptable en los semiconductores compuestos III-V. A continuación desarrollamos la función de onda del electrón, de masa m₀, en esta base de funciones de Bloch

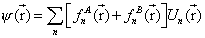(1)

donde el superíndice hace referencia a que la función es distinta de cero sólo en dicho semiconductor. La suma se extiende a todas las bandas de los semiconductores. Puesto que hemos supuesto que la heterounión es abrupta, la función envolvente f debe ser continua en el plano z=0, donde situamos dicha heterounión. Además, por ser plana debe existir invarianza de traslación en la dirección perpendicular a la dirección de crecimiento

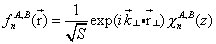(2)

siendo S la superficie de la heterounión. Ordenando las funciones envolventes de las distintas bandas en la dirección de crecimiento en forma de vector se obtiene la siguiente ecuación de autovalores

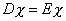(3)

donde las componentes del operador D vienen dadas por

(4)

siendo los elementos de matriz del momento en la base de las funciones de Bloch los siguientes

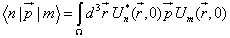(5)

y E_n indica la energía de los bordes de las distintas bandas, que obviamente depende de cada semiconductor. Por simplicidad hemos definido una versión generalizada de la función theta de Heaviside, que vale la unidad en un semiconductor y se anula en el otro.

Queda claro que un tratamiento general de esta naturaleza conduce a ecuaciones complicadas pues todas las funciones envolventes están acopladas a través de los elementos de matriz del momento. El modelo de Ben Daniel-Duke intenta paliar esta dificultad admitiendo que este acoplamiento se puede tratar como un efecto sobre la masa del electrón, que pasa a ser una masa efectiva. Esta masa efectiva depende de la coordenada z pues es diferente en cada semiconductor. Por tanto, en la ecuación (4) se omiten los términos no diagonales (segunda línea de la misma) pero se introduce una masa efectiva dependiente de la posición. La conservación de la corriente de probabilidad en el plano de la heterounión conduce a un operador de energía cinética no convencional, como aparece en ecuación de Ben Daniel-Duke para cada función envolvente

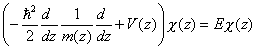(6)

donde hemos supuesto además que el momento transversal es nulo y por simplicidad hemos omitido el subíndice que hace referencia a la banda (hay tantas ecuaciones de este tipo como bandas en el semiconductor). La función V(z) es el valor del borde de la banda en cada semiconductor y es claro que desempeña el papel de una energía potencial.