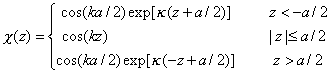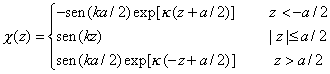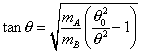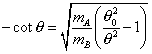Experimento Interactivo 1 de Dispositivos Cuánticos

Estados electrónicos en pozos cuánticos

Las técnicas actuales de crecimiento de semiconductores permiten unir dos materiales diferentes para dar lugar a una heteroestructura. Con técnicas de crecimiento como la epitaxia por haces moleculares (MBE) se puede conseguir que la superficie de separación entre ambos semiconductores sufra sólo alteraciones de una monocapa de un punto a otro, es decir, sean altamente planas. Esta característica es importante porque permite simplificar la descripción del movimiento de los portadores paralelo a dicha heterounión.

Un pozo cuántico se puede obtener cuando se coloca una lámina de un semiconductor (digamos GaAs) entre dos semiconductores de intervalo prohibido mayor (digamos Al_1-xGa_xAs). El modelo de Ben Daniel-Duke permite describir los estados electrónicos de heteroestructuras de GaAs-Al_1-xGa_xAs. Proporciona resultados muy exactos cuando las capas de GaAs no son demasiado estrechas (mayores que unos 100Å) y cuando tratamos con estados cercanos a los bordes de las bandas. Este modelo supone que los estados de la heteroestructura pueden construirse a partir de estados que corresponden a una banda parabólica. Denominaremos E_A y E_B las energías de los bordes de las bandas en ambos semiconductores y V₀ = E_B -E_A el desajuste entre los bordes de sus bandas. Con estas definiciones y en ausencia de interacción espín-órbita se encuentra que la única función envolvente satisface la ecuación 

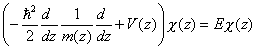(1)

cuando el momento transversal es nulo y z indica la dirección de crecimiento (perpendicular a las láminas de los semiconductores). La funcion V(z) es igual a cero en la lámina de GaAs de espesor 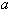mientras que toma el valor V₀ en Al_1-xGa_xAs.

La condición de contorno en z=0 se puede obtener integrando la ecuación anterior en las proximidades de ese plano y se ve entonces que

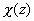y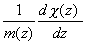

(2)

son continuas. Por tanto, la diferencia de masas efectivas en ambos semiconductores hace que la derivada de la función envolvente presente una discontinuidad en el plano de la heterounión. Conocida la ecuación que satisface la función envolvente pasaremos a aplicar este resultado a un pozo cuántico.

La ecuación para la función envolvente en un pozo cuántico es fácilmente resoluble, y sus soluciones correspondientes a los estados confinados se pueden clasificar de acuerdo con su paridad. Salvo una constante de normalización, resultan ser
 

Pares

 

(3)

 

Impares

 

(4)

 

donde hemos definido los siguientes parámetros reales
 

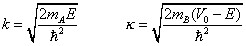
Los correspondientes niveles de energía se obtienen al resolver numéricamente sendas ecuaciones trascendentes
 

Pares

 

(5)

 

Impares

 

(6)

 
 

siendo

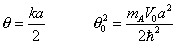
Desarrollo del ejercicio

El sistema elegido para hacer el estudio de los niveles de energía de los estados confinados es un pozo cuántico de GaAs-Al_1-xGa_xAs, donde la fracción del Al varía entre 0 y 0.45, de manera que la aleación es siempre de intervalo prohibido directo. La dependencia de los parámetros con la fracción de Al es

mA=0.067m

mB=(0.067+0.083x)m=mA(1+1.24x)m

V0=0.773x (eV) siendo m

siendo m la masa del electrón libre.

Pulsando sobre el botón se accede a un programa  que permite resolver gráfica y numéricamente las ecuaciones trascendentes (5) y (6) para valores dados de la fracción de Al y espesor de la lámina de GaAs. Las líneas azules representan el valor de las funciones trigonométricas en función de theta mientras que la línea verde es la función raíz cuadrada de la derecha. Los pequeños círculos indican aproximadamente la intersección entre ambas. La gráfica de la derecha representa las correspondientes funciones envolventes (3) y (4) e indica los valores de las energís de los estados confinados.