Método de la bisección

La ecuación (4) del Ejercicio 2 se puede reescribir de la siguiente manera:

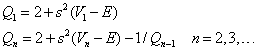(1)

donde n=2,3,... y Q_n es el cociente de las amplitudes de probabilidad en dos nodos consecutivos de la malla. Podemos iterar esta ecuación para un valor arbitrario de la energía E y averiguar si dicho valor es mayor o menor que un determinado nivel de energía del potencial. Para ello utilizamos el hecho de que la función de onda correspondiente a nivel j-simo tiene j nodos, considerando el estado fundamental aquel con j=0 (excluimos los nodos triviales en z=±c).

Notemos que un cambio de signo en la secuencia de amplitudes de probabilidad es equivalente a que un cierto Q_n sea negativo. Por tanto, si utilizando la relación de recurrencia (1) para una cierta energía E encontramos j cambios de signo, entonces podemos concluir que E es mayor que el nivel j-1 y menor que el nivel j. Esto nos permite aplicar el método de la bisección para encontrar los niveles más bajos de energía. En primer lugar determinamos un valor de la energía E_mín tal que la secuencia de valores P_n presente j-1 cambios de signo. A continuación determinamos otro valor E_máx con j cambios de signo. Finalmente hacemos E=(E_máx- E_mín)/2 y determinamos también el número de cambios de signo. Si es igual a j hacemos E_máx=E y si es igual a j-1 hacemos E_mín=E. El proceso se repite hasta que E_máx-E_mín sea menor que la precisión requerida.