Experimento Interactivo 8 de Dispositivos Cuánticos

Aproximación de enlace fuerte a las superredes de semiconductores

En el Ejercicio anterior hemos estudiado los estados electrónicos es una superred ordenada mediante el empleo del teorema de Bloch. Sin embargo, la presencia de campos eléctricos aplicados o la aparición de desorden (intencional o no), conducen a una mayor complejidad del problema puesto que no se cumple la principal hipótesis para aplicar el teorema de Bloch, a saber, la periodicidad del potencial que, en el caso de las superredes de semiconductores, supone la periodicidad de la estructura laminar.

Para abordar un tratamiento más general vamos a olvidarnos de los detalles de la función envolvente en cada pozo cuántico para preocuparnos por su amplitud de probabilidad en cada uno de ellos. Esta magnitud es idéntica en cada pozo en el caso de superredes periódicas, pero no lo será en una situación más general tras la aplicación de un campo o la aparición de desorden. Este último problema es, de hecho, muy complejo pero en el presente Ejercicio abogaremos por la simplicidad asumiendo modelos estrictamente unidimensionales. Esto equivale a suponer que el momento trasversal de los electrones es constante del movimiento, hecho que no se cumple en presencia de rugosidad en las heterouniones. No obstante, a pesar de su simplicidad, veremos que el tratamiento que presentamos a continuación permite profundizar adecuadamente en las propiedades físicas de los estados electrónicos en las superredes de semiconductores.

La idea básica del tratamiento se remonta a los albores de la física del estado sólido y de la química molecular, al utilizar la denominada combinación lineal de orbitales moleculares. En el caso de una superred, el papel de los orbitales lo desempeñan las funciones envolventes de los pozos cuánticos aislados

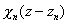(1)

donde el índice n hace referencia al número de pozo, centrado en la posición z_n. De ahora en adelante supondremos, para mayor simplicidad en el presente estudio, que z_n=nL, es decir, los centros constituyen una secuencia periódica. A continuación proponemos como solución de la ecuación de Ben Daniel-Duke una combinación lineal de la forma

(2)

para posteriormente sustituirla en dicha ecuación. Empleando el desarrollo habitual, es decir, despreciando entre otras cosas el solapamiento de las funciones envolventes de pozos cuánticos vecinos, se obtiene la siguiente relación de recurrencia para las amplitudes
 

donde E_n es el nivel del pozo enésimo (puede haber más de un nivel, por lo que el procedimiento se debe aplicar realmente a cada uno de ellos). El parámetro T recibe el nombre de integral de transferencia, y depende de los parámetros físicos de las superred (masas efectivas, alineamiento de las bandas de los semiconductores, espesores de pozos y barreras). En general también depende de los pozos contíguos, que pueden ser diferentes, pero dentro de nuestro propósito de mantener al mínimo posibles complicaciones, vamos a suponer que son constantes. El adelante vamos a utilizar T como unidad de energía, lo que equivale a considerar simplemente la ecuación
 

Cuanto todos los niveles de los pozos tienen la misma energía se trata de una superred periódica. Tomando como origen de energía dicho nivel tendremos E_n=0, y la ecuación anterior se puede resolver mediante el teorema de Bloch. Por el contrario, cuando E_n tomas valores arbitrarios, entonces estaremos describiendo una superred desordenada. Finalmente, si consideramos que E_n=-Fn, estaremos describiendo los estados electrónicos de una superred sometida a un campo eléctrico uniforme.

Desarrollo del ejercicio

Pulsando sobre el botón se accede a un programa  que permite resolver calcular numéricamente C_n para diversas superredes (ordenada y desordenada, con campo y sin campo) dentro de la aproximación de enlace fuerte. Se permite seleccionar el núro de pozos, grado de desorden, valor del campo aplicado y autoestado a representar. La línea azul es la función envolvente de dicho autoestado y en la parte inferior aparece además el potencial en la superred.