Combinación lineal de orbitales

La ecuación de Ben Daniel-Duke para la función envolvente en la superred es

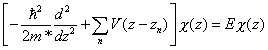(1)

donde la suma se extiende a todos los pozos cuánticos y V(z) representa la discontinuidad de la banda (conducción o valencia) en cada uno de ellos. La función envolvente la escribimos como combinación lineal de las funciones en los pozos aislados

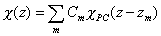(2)

donde cada uno de ellos satisface una ecuación del tipo

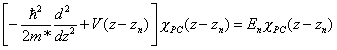(3)

A contunuación sustituimos la solución propuesta (2) en la ecuación (1) y hacemos uso de (3). Finalmente multiplicamos por el complejo conjugado de la función envolvente del pozo k e integramos sobre toda la superred, con lo que obtenemos

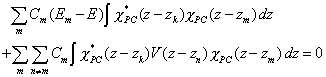(4)

Llegados a este punto estamos en condiciones de introducir la aproximación de enlace fuerte. Supondremos entonces que las barreras son muy anchas, de forma que las funciones envolventes de los pozos individuales son muy localizadas y su solapamiento es despreciable. Esto implica que la primera integral que aparece en (4) es nula salvo que n=k, pues entonces vale la unidad si las funciones están adecuadamente normalizadas. En cuanto a la segunda integral, por los mismos motivos admitimos que es nula salvo que involucre pozos contíos. Llamando -T a dichas integrales (son todas iguales si la superred tiene un único tipo de pozo cuántico), resulta finalmente