Experimento Interactivo 5 de Física del Estado Sólido

Dispersión de electrones en una red lineal

La ecuacón de Schrödinger en una dimensión puede proporcionar una imagen sencilla del comportamiento de los electrones en un cristal. Para ello, consideramos N átomos situados en las posiciones x_n, cada uno de los cuales se supone que crea un potencial de la forma

(1)

Definiendo tendremos entonces

(2)

En lo que sigue vamos a suponer que E sólo toma valores positivos, de forma que q es real, y que tanto como x_n son arbitrarios. Lo que pretendemos es obtener una expresión del coeficiente de transmisión para un electrón empleando el formalismo de la matriz de transferencia, que pasamos a detallar a continuación.

La solución de la ecuación (2) en las regiones donde el potencial es nulo se escribe como

(3)

donde n=1,2,...,N+1 con el convenio y , con las condiciones de contorno a₁=1, b₁=r_N, a_N+1=t_N y b_N+1=0. Aquí r_N y t_N son las amplitudes de reflexión y transmisión respectivamente, de forma que los coeficientes de eflexión y de transmisión serán entonces y .

Empleando las condiciones de contorno que debe verificar la función de onda en los puntos donde están situadas las funciones

			(4)

se llega tras cálculos sencillos a la relación

(5)

donde

(6)

con

(7)

Las ecuaciones (5) y (6) nos permiten escribir

(8)

Usando (5) se tiene que

(9)

Por otra parte, como T_n=P_nT_n-1, es fácil obtener la siguiente relación de recurrencia

(10)

con las condiciones iniciales A₀=1 y A₁=a₁. Por tanto, para cada energía del electrón incidente podemos calcular de manera recurrente usando (9) y (10).

Desarrollo del ejercicio

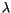Pulsando sobre el botón se accede a un programa que calcula y representa gráficamente en un rango elegido de energías para diferentes valores de L y . Además compara el resultado con las energías permitidas según la relación de dispersión de la cadena infinita

siendo k el momento cristalino.