Experimento Interactivo 8 de Física del Estado Sólido

Estados electrónicos superficiales

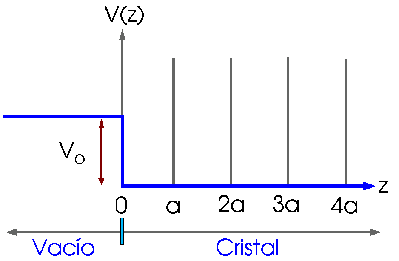
En problemas tales como catálisis, reactividad o crecimiento epitaxial de los sólidos, el papel primordial lo desempeña la superficie. Un modelo sencillo de superficie aparece esquematizado en la Figura 1. En este modelo se supone que el potencial en el interior de un sólido monodimensional es una serie de funciones delta equiespaciadas, mientras que el vacío se representa mediante un potencial constante. En consecuencia, el potencial se puede escribir como

(1)

Aquí es la función paso de Heaviside (toma el valor unidad cuando su argumento es positivo y se anula cuando es negativo), a es el parámetro de red y P es la constante de acoplamientode cada potencial atómico.

Figura 1: Esquema del potencial V(z).

Cuando no consideramos el efecto de la superficie, es fácil encontrar la relación entre el momento cristalinodel electrón, k, y la energía del mismo, E,

(2)

para energías entre 0 y V₀. Cuando el momento cristalino es real, el electrón tiene una energía permitida, es decir, su energía pertenece a una banda y la función de onda es extendida. Esto es válido en el caso de cristales infinitos. Sin embargo, la superficie hace que el teorema de Bloch no sea válido en sentido estricto y el momento cristalino puede ser de la forma

(3)

Esta relación permite la existencia de estados superficiales con energía en el intervalo prohibido del cristal infinito. La relación entre el parámetro y la energía de estos estados se puede encontrar insertando (3) en (2), con lo que se obtiene

(4)

La solución de la ecuación de Schrödinger en el vacío () debe ser exponencialmente decreciente cuando , esto es

(5)

donde A es una constante y es real. La función de onda en el cristal es

			(6)

siendo B y B' constantes y, por brevedad, hemos definido

Si k es complejo, de la forma dada en (3), el segundo término de (6) diverge cuando , de manera que debemos tomar B'=0 para obtener soluciones físicamente aceptables. En consecuencia, la solución en la primera celda unidad () será

(7)

con

Para obtener la energía del estado superficial imponemos la continuidad de la función de onda y su derivada en . Utilizando además que el momento cristalino debe ser de la forma que aparece indicada en (3), se llega finalmente a que

(8)

donde y .

La ecuación (8) nos proporciona las soluciones E reales en el intervalo [0,V₀] que corresponden a estados superficiales con energía en un intervalo prohibido. Se trata de una ecuación trascendente que puede ser resuelta sin dificultad mediante el método de Newton. Si representamos ambos términos de la ecuación en función de podemos ver que existe una solución entre 0 y siempre que , mientras que siempre existe una solución de la ecuación (8) en cada intervalo . Sin embargo, no todas la soluciones de dicha ecuación son físicamente aceptables ya que, además, se debe cumplir la denominada condición de existencia. En efecto, dado que hemos impuesto , no es difícil comprobar que

(9)

Por tanto, debemos comprobar también que, mediante la adecuada elección de parámetros, las raíces de (8) corresponden efectivamente a estados superficiales, que deben satisfacer (9).

Para estudiar las propiedades de localización de los estados superficiales definimos la densidad de probabilidad relativa P(z)como

(10)

cuyo significado físico es bastante claro. Dado que ya hemos resuelto el problema, esta magnitud se puede encontrar sin dificultad

(11)

donde , y se puede obtener de (4).

Desarrollo del ejercicio

Pulsando sobre el botón se accede a un programa que calcula y representa gráficamente la función de onda del estado superficial y determina su energía. Se puede seleccionar tanto el valor del parámetro de red como la energía del vacío. La línea vertical de la gráfica indica la posición de la superficie del cristal.