Experimento Interactivo 3 de Física Estadística

Transformaciones del Panadero y de Arnold

Muchas propiedades del espacio de las fases pueden entenderse con modelos dinámicos sencillos, como los que introduciremos en este experimento. Son las llamadas Transformación del Panadero (baker's transformation) y Transformación de Arnold (o Arnold's cat map). Ambas actúan sobre un espacio de fases bidimensional, transformando un punto sobre el cuadrado unidad, en un punto transformado con una aplicación que conserva la medida en el espacio de las fases . Ambas transformaciones son ergódicas.

Transformación del Panadero

Esta transformación actúa sobre la región , contrayendo la dirección en un factor 1/2 y expandiendo la dirección en un factor 2. A continuación, la región con se corta y se coloca en la parte superior del intervalo . La transformación de un punto es:

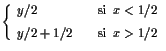Puede verificarse de manera sencilla que esta transformación conserva el área del espacio .

El applet que incluimos aquí ilustra la transformación del panadero. Puede escogerse como dato incial para la iteración la cara de un gato, un círculo o una nube de puntos aleatorios en el cuadrado . Se elige el dato incial y se pulsa el botón . Para aplicar la transformación del Panadero, pulse el botón . Después de una cuantas iteraciones, los puntos que componen las figuras se han distribuido de manera uniforme sobre el espacio, llenándolo en su totalidad. Esta transformación es ergódica y mixing.

Cuando se pulsa el botón repetidas veces (unas 50 veces), se observa que los puntos ya no cubren el espacio de maera uniforme, sino que se forman bandas o regiones que evolucionan hasta el origen. Ello se debe a la precisión finita con la que se realizan los cálculos numéricos.

Transformación de Arnold

La transformación de Arnold forma parte de una clase más complicada de transformaciones llamadas automorfismo torales. Son transformaciones lineales del cuadrado unidad en sí mismo con condiciones de contorno periódicas, definidas a través de una matrix , que transforma el punto en el según:

(1)

La matriz debe tener determinante 1, esto es, det que nos garantiza que dicha transformación conserve el área en el espacio , dado que el determinante no es m'as que el Jacobiano de la transformación de . Para que la transformación (1) sea ergódica es necesario que los autovalores de sean reales y diferentes de 1. Para garantizarlo, se suele exigir que los elementos de sean enteros positivos. Bajo estas condiciones, los autovectores de son ortogonales, y existe un autovector mayor que 1 y otro menor que 1. La dirección asociada al autovalor mayor que 1 se expande y la asociada al menor que 1 se contrae. Ciertas matrices que no satisfacen estas condiciones dan comportamientos no ergódicos (pulsa aquí).

Todo ello se observa en este Applet, similar en su funcionamiento al de la transformación del panadero. Aquí, sin embargo, se pueden elegir tres elementos de la matriz (el cuarto viene fijado por la condición det ). Los valores y (que implican ) son los usuales que introdujo Arnold.

De nuevo puede observarse como los puntos se reparten uniformemente sobre el cuadrado tras unas pocas iteraciones, aunque el número de las mismas depende de los valores de los elementos de la matriz . De nuevo, tras un número elevado de iteraciones, los puntos colapsan al (0,0) debido a redondeos causados por la precisión finita de los cálculos.

Bibliografía: J.R. Dorfman, An Introduction to Chaos in Nonequilibrium Statistical Mechanics, Cambridge Lecture Notes in Physics (1999).