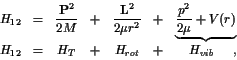Experimento Interactivo 6 de Física Estadística

Moléculas Diatómicas

El objeto de esta práctica es el estudio de las propiedades de un gas de moléculas diatómicas, cuyo hamiltomiano para el par de átomos (1 y 2) que componen la molécula es:

(1)

Este Hamiltoniano puede separarse en dos partes: la parte debida al movimiento del centro de masas de la molécula y la parte debida al movimiento de los átomos respecto al centro de masas. Para ello utilizamos la transformación a coordenadas relativas:

(2)

con lo que el hamiltoniano (1) se reescribe como:

(3)

donde es la masa total de la molécula y es la masa reducida. Así que para la función de partición de una molécula tenemos que:

y la de moléculas se puede escribir como:

A partir de esta función de partición se calcula el calor específico por partícula como:

donde las derivadas parciales que aparecen se deben tomar a y constante.

Pasemos a calcular las tres funciones de partición que aparecen. La función de partición traslacional es la de una partícula libre en 3 dimensiones:

que da una contribución al calor específico:

Vibración

La parte vibracional incluye el potencial de interacción interatómico. Si suponemos que los átomos vibran alrededor de las posición de equilibrio con pequeña amplitud (lo que hemos asumido implícitamente en (3)), podemos desarrollar el potencial en serie de potencias alrededor de , obteniendo:

donde el término en derivada primera, es nulo porque está evaluada en , que es la posición de equilibrio en la que es mínimo. Así pues, el potencial se puede aproximar por un potencial armónico de frecuencia . Por tanto, el hamiltoniano de rotación se reduce a:

cuyos niveles de energía cuantizados según:

y la función de partición (que se puede calcular):

(4)

donde hemos definido la temperatura característica de vibración como:

que suele ser del orden de cientos a miles de kelvins. Las contribuciones al calor específico son:

Rotación

La parte rotacional, incluye el operador momento angular , cuyas autofunciones son los armónicos esféricos, con ecuación de autovalores: , con degeneración . Entonces la función de partición es:

(5)

de donde podemos definir la temperatura característica de rotación como:

que varía entre décimas de kelvin a unos pocos kelvins (excepto el hidrógeno). Para temperaturas bajas comparadas con , , podemos calcular porque sólo los primeros términos de la serie (5) son importantes. Por el contrario, a temperaturas altas, , todos los términos en (5) deben ser sumados.

En estos límites las contribuciones al calor específico pueden ser calculadas, obteniéndose:

El applet en Java permite introducir las temperaturas de rotación y traslación y el programa calcula el calor específico por partícula (en unidades de ) representado frente a . El applet dibuja dos líneas verticales, correspondientes a y y tres horizontales, que son las contribuciones de la parte traslacional (3/2), la rotacional (1) y la vibracional (1) cuando las temperaturas son mucho mayores que la rotacional y la vibracional respectivamente.

Si las temperaturas características están bien separadas, como sucede en la moléculas diatómicas reales, pueden observarse claramente las contribuciones de los tres hamiltonianos. El calor específico debido a la rotación muestra un máximo alrededor de .

Las temperaturas características para algunas moléculas diatómicas son:

	H	N	CO	NO	O	Cl	Br	K
	85	2.9	2.8	2.4	2.1	0.35	0.12	0.081
	6200	3340	3070	2690	2230	810	470	140

Pulsa aquí para ver una gráfica con las medidas experimentales del calor específico a presión constante de los gases HD, HT y DT, donde D representa el deuterio y T el tritio, frente a la temperatura. La relación entre y para gases ideales es: y, por ello, los resultados para están desplazados una unidad.

En esta gráfica se comparan los resultados de la contribución vibracional al calor específico, Ec. (4) en función de T/ para varios gases.

Para moléculas triatómicas el análisis anterior se complica notablemente. Por ejemplo, el CO tiene 4 modos normales de vibración. El texto de J.Kestin y J.R.Dorfman (A Course in Statistical Thermodynamics, Academic Press, 1971) incluye una gráfica con el calor específico de dicha molécula.