Experimento Interactivo 1 de Física del Estado Sólido

Evaluación de la constante de Madelung

La constante de Madelung nos permite determinar la energía de interacción de un ión con los restantes iones en un cristal iónico. En un cristal iónico con estructura cúbica como el NaCl, la constante de Madelung se define como

(1)

donde la prima en la suma indica la exclusión del término l=m=n=0. 

La forma de agrupar los distintos términos de la serie (1) influye decisivamente en la convergencia más o menos rápida de las sumas parciales hacia el valor de dicha serie. En el caso del NaCl el método más sencillo, aunque no el más efectivo, es considerar cubos de lado 2kR, siendo k un entero positivo. En la Figura 1 se muestra el primero de estos cubos. 

Figura 1: Estructura cristalina de un cristal iónico como el NaCl.

  Con esta estrategia, la serie (1) puede escribirse como  

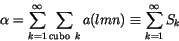(2)

siendo a(lmn)=(-1)^l+m+n+1(l²+ m²+n²+1)^-1/2 y donde hemos definido

			(3)

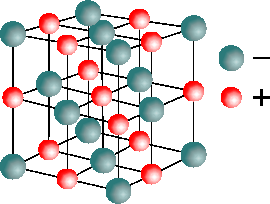
La serie (2), con los coeficientes dados por (3), converge lentamente, como veremos en la simulación numérica. Sin embargo, como propuso Evjen, la convergencia de las sumas parciales se puede mejorar apreciablemente considerando grupos de átomos cuya carga total sea nula. Para hacerlo debemos considerar la contribución efectiva de cada ión a la carga del cubo (1/2, 1/4 y 1/8 si está situado en una cara, arista o vértice, respectivamente). La forma de proceder analíticamente es reagrupar términos en (3) y escribir  

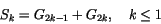(4)

donde por brevedad hemos introducido las siguientes magnitudes

			(5)

con k mayor o igual que 2. Para obtener una serie más rápidamente convergente definimos

			(6)

de forma que  

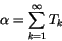(7)

Desarrollo del ejercicio

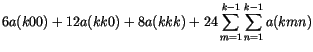
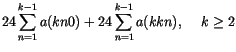
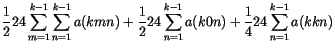
Pulsando sobre el botón se accede a un programa  que calcula y representa gráficamente la constante de Madelung en función del numero de términos que se van considerando en las expresiones (2) y (7). Cabe destacar que la convergencia es realmente pobre cuando se emplea el primer método (2) mientras que es realmente buena utilizando el segundo método (7), ya que con muy pocos términos se alcanza el valor 1.74756.